Back to Main Page

Earthquake Load & Building Dynamics

Structures should be robust enough against the action of various kinds of forces as: Gravity Load, Wind Load, Blast Load & Earthquake Load. Along with the thorough understanding of nature of various kinds of loadings, properties of structures also plays a vital role in structural response. Following describes the nature of various loadings and structural dynamics with special attention on Building Dynamics.

 

Types of Loading

Earthquake Loading

Building Dynamics

 

Types of Loading

Gravity Load is the load due to self weight of a structure itself and its occupants. Self weight of the structure is static in nature and can be estimated more accurately. Also, load due to occupants/occupancy can be estimated with certain degree of accuracy. Gravity load acts along the direction of gravity: vertically downward. That’s why structural design against the Gravity Load Case doesn’t pose much hindrance to Structural Engineers. Thereby structures are mostly safe under this loading. Collapse cases in Gravity loading had been observed only in few of the cases.

Unlike Gravity Loading, the Earthquake Loading, which is dynamic one and very much uncertain in nature is a major challenge to Structural Engineers worldwide. Its uncertainty regarding its occurrence, magnitude, frequency content and duration makes it quite complicated to estimate it.

 

Earthquake Loading

Earthquake load on any structure is basically due to inertial property of the structure itself. Inertia, by its virtue, is an ability of any object to remain in state of rest unless acted upon by an external force. During earthquakes, as the ground shakes, lower part of structures is enforced to move with ground, whereas its upper part by virtue of inertia tries to maintain its original state of rest. Accordingly, there exists two different deformation behaviors between lower and upper parts of the structure; hence forces are induced in it.

Inertial force is proportional to mass of the structure (Eqn-1). So greater the mass of the structure, higher will be the inertial /earthquake force acting on it and vice-versa.

 

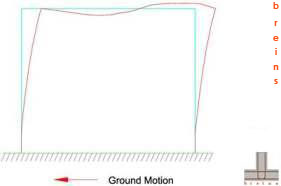
Fig-1 (Deformation of an one storeyed building frame model under the earthquake load due to inertial property of building mass)

 

As from the Newton's Second Laws of Motion, force (F) on any body is product of its inertial mass (m) and acceleration (a) induced in it. In formula,

(1)

 

In earthquakes, for the given type of structure, acceleration response is primarily dependent on frequency content of imposed ground motion, its degree of Flexibility along-with boundary condition at base. Flexible Structures undergo lower acceleration values than if it were stiffer ones for the given ground acceleration of normal frequency content.

 

Building Dynamics

Not only the uncertain nature of earthquake loadings, structures themselves possess different dynamic characteristics according to their configuration. Response of structures vary as per their dynamic properties even for the same earthquake within the same locality. Such inherent properties of structures are studied in Structural Dynamics.

Stuctural properties as Flexibility, Stiffness and Mass; and their distribution within the structural system are of utmost importance.

Structural property called Flexibility primarily depends on its ratio of height to width for the given boundary condition at its base. Higher this ratio more flexible it is. Flexibility refers to ability of structures to deform under the applied load. More it deforms, more flexible it is. Due to this, in most of the building structures, it is not possible to have a single acceleration value for the entire structure's motion. Acceleration induced in a building structure due to ground motion at its base varies along its height. In buildings of regular vertical configuration, ground acceleration is magnified towards the building's top with increase in lateral displacement. Refer expression (3) below.

The opposite physical behavior to Flexibility is called Stiffness (K). Stiffness, simply is a measure of resistance against deformation under the application of load. Taller the building more flexible it is and less stiff it becomes. In summary, for the given ground motion and local site conditions, earthquake load on any structure is basically a function of its Mass (m) and Stiffness (K). This property can be quantized by the Time Period (T); which for any single degree of freedom structure undergoing Sinusoidal Periodic Motion is;

 

(2)

 

Time Period (T) is used to determine the time required to complete one complete cycle by a system undergoing periodic motion. For instance, simple harmonic motion of a simple pendulum clock (Fig-2). Vibratory acceleration (a) of such motion is given by;

 

(3)

 

Where y represents the Displacement of the Mass (m) of the system with respect to center of oscillation.

 

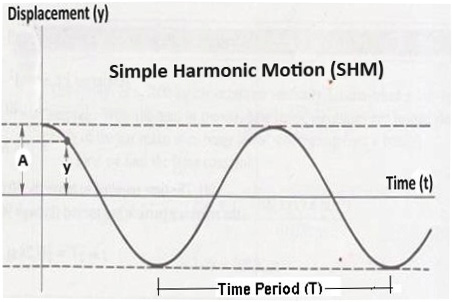
Fig-2 (Graphical Representation of Simple Harmonic Motion showing Amplitude of Motion (A), Time Period of Vibration (T) & Diplacement (y))

 

In Building Dynamics, Time Period (Fig-2) is defined as a time required for a building to complete one complete cycle of vibratory motion; when displaced & released freely (Free Vibration). Such motion could be Damped or Undamped one. Time Period in case of Damped motion is called Damped Period of Vibration (Td) and for Undamped motion, it is called Natural Time Period (Tn). Natural Time Period (Tn) is discussed in detail next.

Time Period of the Building Structure undergoing Free Vibration provided that no decay in motion occurs (Undamped) is reffered as Natural Time Period (Tn). Natural Time Period refers that it is an inherent property of any structure which is independent of external factors. Natural Time Period (Tn) of any structure is a single useful parameter regarding its performance in external excitations.

Earthquakes make buildings with longer Natural Time Period (Tn) to vibrate with lower acceleration response resulting in lower earthquake forces (Eqn-1) to that of the Short Natural Time Period Structures (Stiff Structures); provided that both the structural and geological configuration are similar. Above all these factors, Frequency Content of the earthquake excitation shall not be disregarded.

Time Period of a system can be increased by decreasing the Stiffness (K) and also by enhancing its Damping Characteristics. Stiffer structures possess lower value of Time Period and hence higher acceleration. Damped Time Periods (Td) are always longer than its Undamped case (Tn) resulting in lower amplitude of motion (y) and thereby the lower acceleration.

It should be noted that for building structures, multiple values of such Time Periods corresponding to different vibration modes are possible. It is basically true for flexible structures and building structures that have variations in storey stiffness, mass.

more